10.3 量的変数の関係
10.3.1 Excel による散布グラフとバブルチャート

本ウェブページは『超入門 はじめてのAI・データサイエンス』第10章の10.3に対応したコードを埋め込んでいます。まずは,量的データの 2変数 の 関係 を把握する手段として,散布図について説明します。

動画ではExcelによる散布図に加えて,途中で バブルチャート の作り方も紹介していますが,バブルチャートが使用できないPC環境もあるようです。過去にはPCが固まってしまったという報告もあったため,バブルチャートを試す前には,必ずファイルの保存またはバックアップを取っておきましょう。

ここでのタスクは,年齢とカード利用回数は関係があるかを探索することです。散布図では,横軸(X)も縦軸(Y)も 量的データ になります。X軸は 独立変数 または 説明変数,Y軸は 従属変数 または 目的変数 でしたが,この場合,年齢によってカードの利用回数は変わるかもしれませんが,カードの利用回数によって年齢は変わらないため,X軸が年齢,Y軸がカード利用回数となるのが適切です。
Mac × 日本語
Windows × English

それでは動画の手順です。シートから 年齢 と カード の列を選びます。集計行まで選ばないように注意します。Excelは自動的に左側にある列を X軸 としますが,どちらの列を X軸・Y軸 にするかはいつでも切り替えられます。「挿入」→「グラフ」→「散布図」 を選び,可視化による探索的分析としてデータの特徴を視覚的に確認します。グラフから,ざっと 3つの点 を確認します。

第1に,関係性の傾向です。動画の場合,全体に右上がりの分布になっていて,年齢とカード利用回数が 正の関係,つまり,年齢が高いほどカード利用回数が多い傾向が見て取れます。関係性は常に直線的とは限りませんが,直線的な関係の場合には,右下がりの分布は 負の関係,XYに関係がない場合は,Yの平均値(X軸に平行な水平線)を中心に値が分散しているプロットになります。
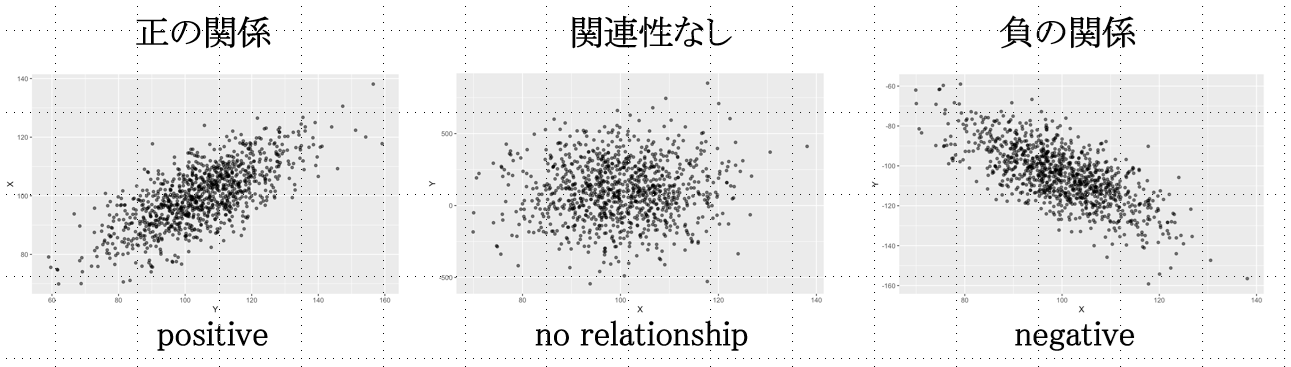

第2に,分布の範囲や集中度などを確認します。動画の場合,年齢は 18歳以上 しかデータにないことがわかります。

第3に,外れ値を確認します。これがなぜ問題になる可能性があるかというと,たとえば下図のように,ほとんどのプロットがランダムに分布しているのに,外れ値(下図の赤い丸)によって,まるで右上がりの 正の関係 があるかのような統計量が出てしまうことがあるからです。


悪い場合には,この外れ値は異常値ですらなく,データクリーニングの不足 による誤ったデータが入り込んでいるケースである場合もあります。なので,分析をする前に可視化 をしてデータを確かめておくことが大切なのです。なお特定の値を外れ値として分析から外すかどうかは 分析者の判断 で,外す場合には 報告書に記しておく必要 があります。

X軸の最小値を 15歳 にします。つぎに動画では,外れ値が誰であるか を確かめています。ラベルオプションで Y値 のチェックを外して,セルの値 にチェックを入れ,範囲に 氏名のセル範囲 を指定して,外れた値の個人を特定しました。確認後は,データラベル を消しておきます。そして 軸ラベル を入れました。

動画では 3変数の関係を把握する バブルチャート に変えています。バブルチャートは 3つ目の変数 を入れることができる便利な図で,ここではその変数として Amount(動画では「金額」) を使っています。

以下にバブルチャート作成手順をまとめておきました。参考にしてください。
- グラフの種類から バブルチャート を選びます。
- データのバブルサイズがすべて1になっている状態を消去して,Amountのセル範囲 を指定します。
- バブルが大きすぎて視認しづらいため,バブルのいずれかをクリックして 書式設定 を開きます。
- バブルの大きさ を小さく調整します。
- 色 を変更し,タイトル を付けて完成です。
10.3.2 相関

それでは,\(XY\) に 正・負の関係があるかどうか をどのように数値にすれば良いでしょうか? \(x\) の偏差 × \(y\) の偏差の積を考えてみましょう。
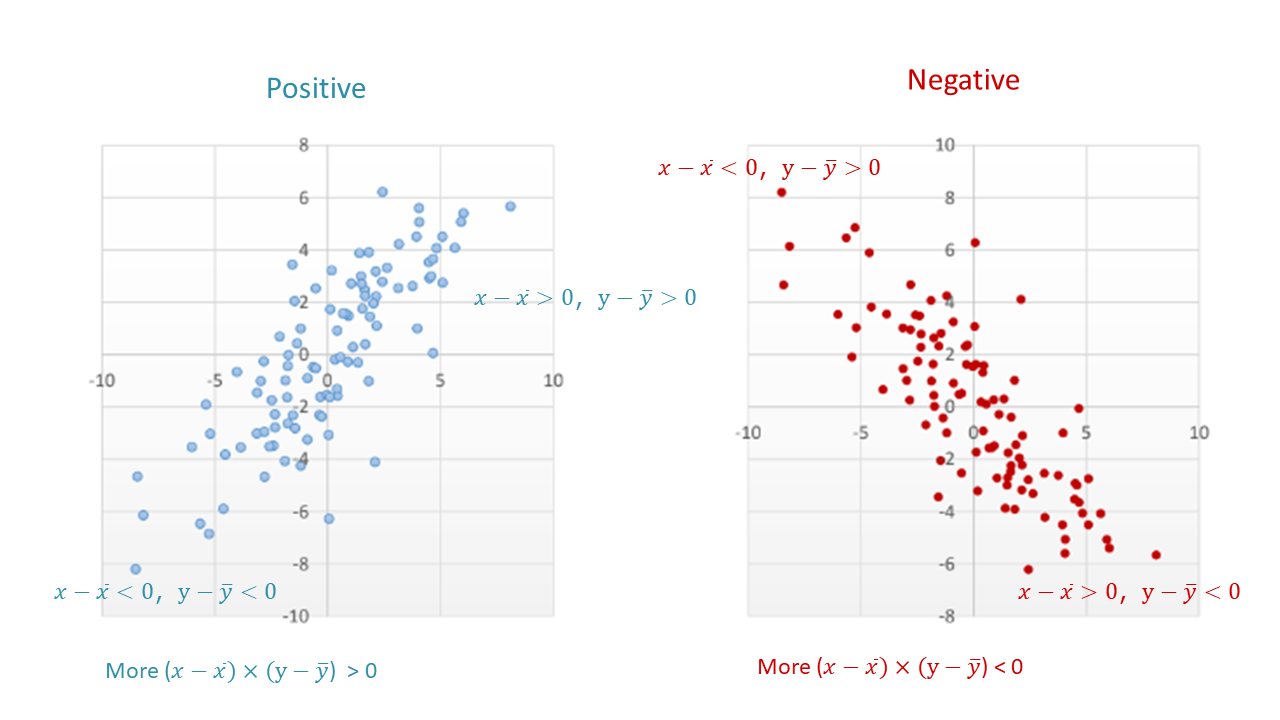

上図に見るように,平均値を中心として4つの区画に分けてみると,右上がりの 正の関係 のときには上式が正になる,つまり左下と右上の区画に入るプロットが多く,右下がりの 負の関係 のときには上式が負になる,つまり左上と右下の区画に入るプロットが多くなります。

その平均,つまり総計して \(n\) で割った \(s_{xy}\)(下式)を 共分散(covariance) と言い,これが正の値のときには 正の関係,負の値のときには 負の関係 を示します。ただ,値の大きさは 単位に依存 するので,関係性の大きさを判断するのには不向きです。
\(s_{xy}=\frac{\sum{(x_i-\overline{x})×(y_i-\overline{y})}}{n}=\frac{偏差の積の総和}{個数}\)

標準偏差で割れば 単位の大きさが調整 されて比較可能になります。共分散 を \(x\) の標準偏差と \(y\) の標準偏差で割ってみましょう。そうすれば 関連性の大きさ を比べることができます。

これがピアソンの 相関係数(correlation) \(r\) で,2つの量的変数の関係を示すのに多用される統計量です。
ピアソン相関係数: \(r=\frac{s_{xy}}{s_xs_y}\)

ExcelのCOVARIANCE.S は標本から母集団の共分散を推定する 不偏共分散 で,上記の共分散の数式の分母を \(n\) ではなく,\(n - 1\) にしたものとなります。
Mac × 日本語
Windows × English
10.3.3 線形回帰

\(X\) が大きいほど \(Y\) が大きくなる 正の相関,\(X\) が大きいほど \(Y\) が小さくなる 負の相関 に見られるように,\(X\) と \(Y\) に直線的な関係があるとき,最小二乗法でプロットの中心を通る線を引いたものを 回帰直線 と言います。このように \(Y\) を \(X\) に回帰させるのに直線を使うモデルを 線形回帰モデル(linear regression model) と言います。その直線を表す数式を 回帰式 と言います。
標本回帰式: \(y_i=b_0+b_1x_{1i}+e_i\)
予測回帰モデル: \(\hat{y_i}=b_0+b_1x_{1i}\)
母回帰式: \(y_i=\beta_0+\beta_1x_{1i}+\varepsilon_i\)

標本回帰式 の数式は,\(i\) ケース目のデータの点のプロット位置を表しています。最後の \(e_i\) は,回帰直線から予測される予測値からのケース \(i\) のズレ(残差)を表しています。

標本予測式 の数式は,標本上の回帰式の直線を表しています。ハット(^)の記号は 予測値 を表します。\(b_0\) が 切片,\(b_1\) が 傾き で,この \(b_1\) を 回帰係数 と言います。

母回帰式 における係数 \(b_0\),\(b_1\) は母集団における パラメータ を表しており,最後の \(\varepsilon\) は 誤差 です。標本から計算される \(b_0\) を \(\beta_0\) の推定値,\(b_1\) を \(\beta_1\) の推定値とします。ちなみに,回帰分析を行うときには 重回帰分析 を行うことが一般的です。その場合には複数の \(X\)(この場合 \(n\) 個)が投入されて,下のような式になります。
線形重回帰モデル: \(y_i=\beta_0+\beta_1x_{1i}+\beta_2x_{2i}+\beta_3x_{3i}…+\beta_nx_{ni}\)

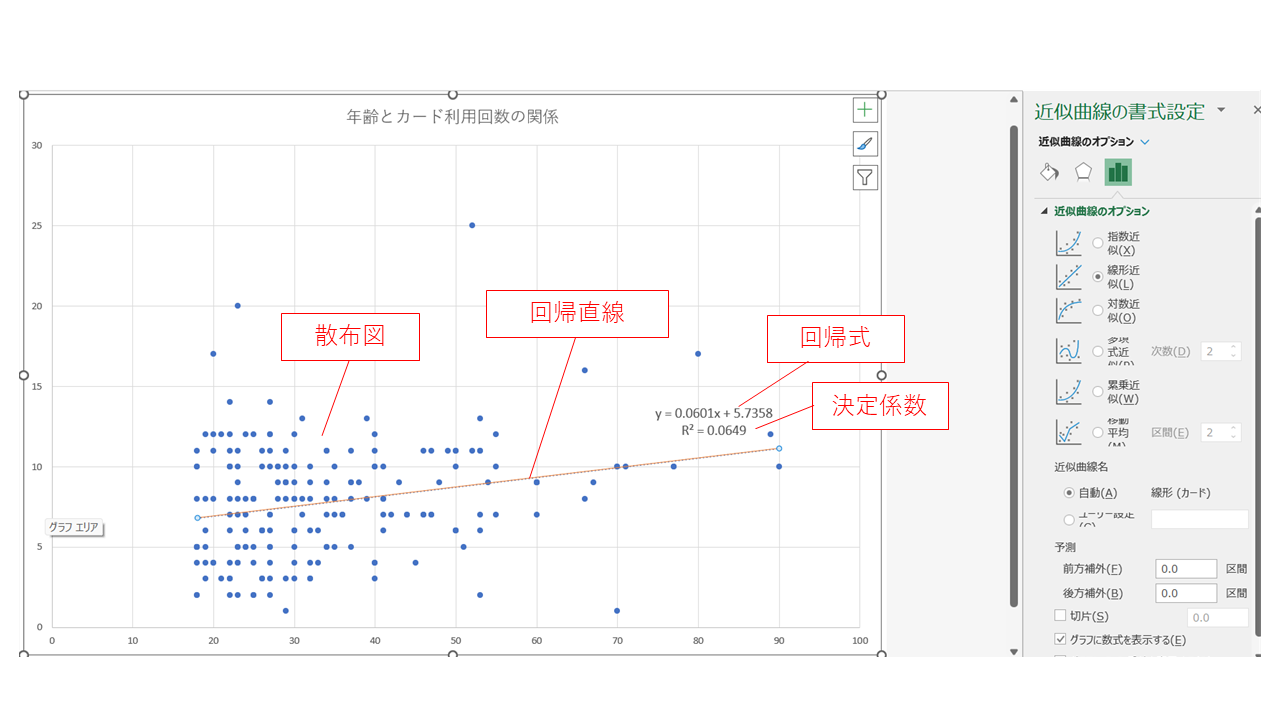
下の動画では 回帰直線 を作り,回帰式 と \(R^2\) を確認しています。動画のデータとみなさんのデータは違いますが,Excelの操作は同じです。グラフをクリックして (Win) + [プラス] 印,(Mac) グラフ要素の追加から,近似曲線 を選び,近似曲線のオプション を「線形」にします。書式設定 で \(R^2\) を表示させましょう。
Mac × 日本語
Windows × English

\(R^2\) は 決定係数 といい,変数の分散を説明できるほど大きな値になります。決定係数 \(R^2 = 0.0649\) ということは,\(X\) によって説明できる \(Y\) のばらつきが全体の 6.5% だという意味です。極端な話,仮に各点が回帰線の上にぴったり載っていたとしたら,\(X\) によって \(Y\) の値のばらつきをすべて説明できたということになり,その場合決定係数は 1.00(100%)となるわけです。

それぞれの近似曲線の数式がどうなっているかも,グラフに数式を表示する にチェックを入れて確認することができます。動画では,グラフタイトルを「年齢とカード利用回数の関係」とし,ワークシート名を Scatter にしました。これで今回の散布図の完成です。

単回帰の場合の決定係数 \(R^2\) は,ピアソンの相関係数 \(r\) の二乗となります。

回帰係数\(b\)は\(\beta_1\)の推定値ですが,この場合のように回帰係数が \(r=0.06\)ぐらいでは,\(\beta_1 = 0\)という帰無仮説通りの(つまり,回帰直線に傾きがない)母集団からかなりの確率で得られるような数値であるかもしれません。

ここで前回学んだt分布を応用し,\(\beta_1 = 1\)の95%信頼区間に0が含まれれば,有意水準 \(\alpha = 0.05\)で回帰係数(傾き)は統計的に有意とは言えないことがわかります。以下ではPythonによる相関と線形回帰を紹介します。
10.3.4 Python による相関

ここでは,SQLで作成したinvoiceというテーブルをPythonで読み込んで,そのamountとdollarの相関を算出します。

Colabはマウントし(第6章参照),SQLiteと接続しておきます(第8章参照)。テーブルinvoiceの含まれるMy_first_AI_DS.db(あるいは自分で付けた名前のデータベースファイル)(第7章参照)をColab Notebooksのdataに入れておきます。

ライブラリpandasもpdというエイリアスで読み込み,そのread_sql関数でデータを読み込んだものをdf6というデータフレームに格納します(第5章参照)。下記はコード1です。
コード 1
import sqlite3
import pandas as pd
conn = sqlite3.connect("/content/drive/MyDrive/Colab Notebooks/data/My_first_AI_DS.db")query = "SELECT*FROM invoice;"
df6 = pd.read_sql(query, conn)
display(df6)
下記はコード2です。queryやconnを用いて処理を分割しない場合のコードです。
コード 2
df6 = pd.read_sql('SELECT * FROM invoice;', sqlite3.connect("/content/drive/MyDrive/Colab Notebooks/data/My_first_AI_DS.db"))
display(df6)
df6ができたので,下記のコード3では,pandas.DataFrame.corrをデータフレーム型のオブジェクトであるdf6のメソッドに用いて,amountとdollar列の相関を算出します。
コード 3
r = df6["amount"].corr(df6["dollar"])
print(r)10.3.5 Python による線形回帰

ここでは,第8章で可視化したペンギンのヒレの長さと体重の関係を回帰分析により検証します。

下記のコード4では,必要なライブラリやデータを読み込み,欠損値を削除して,ペンギンデータをdf2とします。
コード 4
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
!pip install japanize-matplotlib
import japanize_matplotlib
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
df = sns.load_dataset("penguins")
df2 = df.dropna()
df2.head()
下記のコード5の回帰分析では,scikit-learnライブラリのLinearRegressionを使用します。
コード 5
lr = LinearRegression()
x = df2[["flipper_length_mm"]].values
y = df2["body_mass_g"].values
lr.fit(x,y)
y_pred = lr.predict(x)
下記のコード6で,回帰係数,切片,決定係数を表示させます。
コード 6
print("回帰係数 = ", lr.coef_[0])
print("切片 = ", lr.intercept_)
print("決定係数 = ", r2_score(y,y_pred))
下記のコード7では,最小二乗法のライブラリで主な統計量を表示します。
コード 7
import statsmodels.api as sm
x2 = sm.add_constant(x)
est = sm.OLS(y, x2)
est2 = est.fit()
print(est2.summary())