10.1 仮説にかんする用語

本ウェブページは『超入門 はじめてのAI・データサイエンス』第10章の 10.1, 10.2 に対応したコードを埋め込んでいます。ここでは 2つの変数の関係 ,\(x\),\(y\) の両方または片方が 質的データ である場合について,統計の基礎的な部分を抜粋してお伝えします。

変数の関係は一般に変数 \(x\)と\(y\) の関係として表されます。 \(x\)は仮説において原因となる方の変数で,独立変数 または 説明変数 と呼ばれます。一方 \(y\) は仮説において結果となる方の変数で,独立変数が与えられたときにその値に従属して値が動くので 従属変数,または説明変数が説明しようとする目的であるので 目的変数 と呼ばれます。
| 変数 | 意味 | 呼び方 |
|---|---|---|
| \(x\) | 仮説において原因となる変数 | 独立変数,説明変数 |
| \(y\) | 仮説において結果となる変数 | 従属変数,目的変数 |

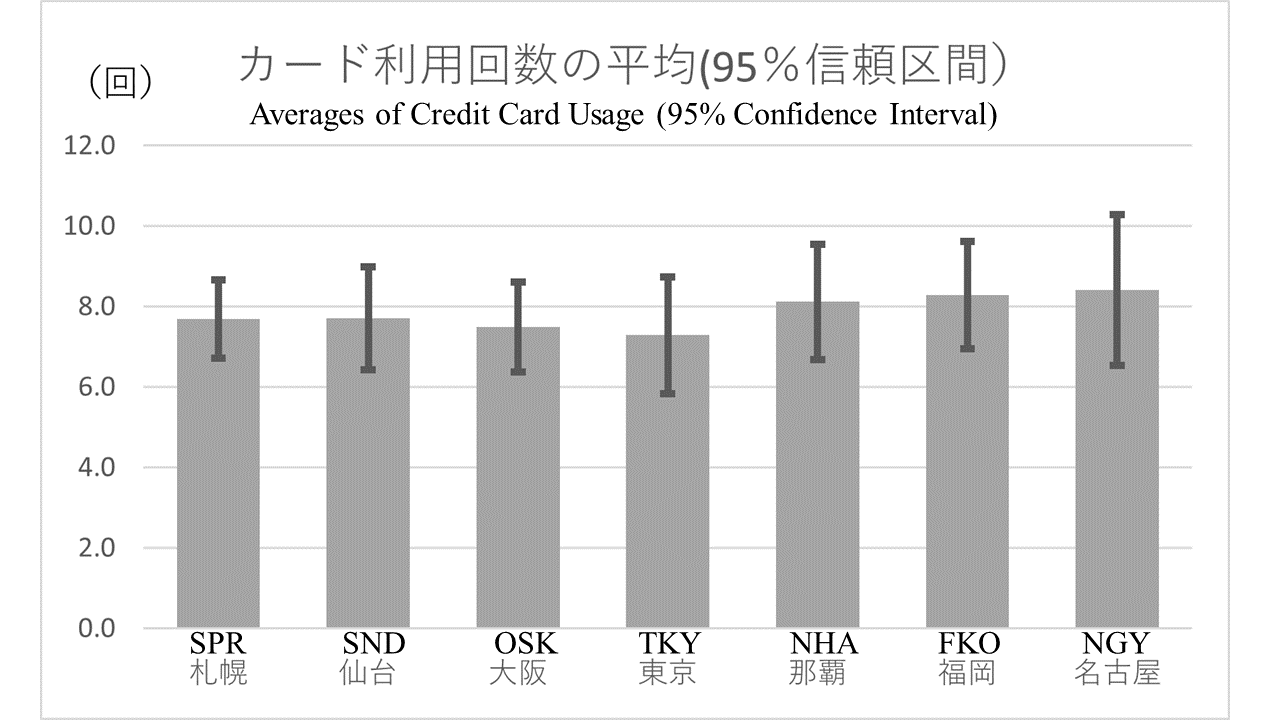
\(x\) と \(y\)がともに質的変数の場合はクロス集計表,\(x\) が質的変数で \(y\) が量的変数の場合は平均の比較になります。これについては,下の短い動画を参考にしてください。
日本語
English subtitles in YouTube: Click on the gear button for "Settings" > Subtitles > Auto-translate > Choose "English" -> Click on CC Button for Subtitles/closed captions